Papers

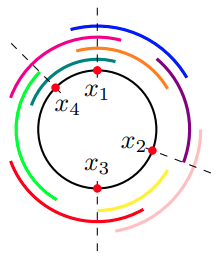
Piercing Numbers in Circular Societies

Kristen Mazur, Mutiara Sondjaja, Matthew Wright, and Carolyn Yarnall

to appear in the Contemporary Mathematics volume Mathematical Analyses of Decisions, Voting, and Games.

preprint on arxiv.org (2022)

Abstract Bibtex

In the system of approval voting, individuals vote for all candidates they find acceptable. Many approval voting situations can be modeled geometrically, and thus geometric concepts such as the piercing number have a natural interpretation. In this paper, we explore piercing numbers in the setting where voter preferences can be modeled by congruent arcs on a circle — i.e., in fixed-length circular societies. Given a number of voters and the length of the voter preference arcs, we give bounds on the possible piercing number of the society. Further, we explore which piercing numbers are more likely. Specifically, under the assumption of uniformly distributed voter preference arcs, we determine the probability distribution of the piercing number of societies in which the length of the arcs is sufficiently small. We end with simulations that give estimated probabilities of piercing number for societies with larger voter preference arcs.

@misc{Mazur_EtAl_2022,
  title = {Piercing Numbers in Circular Societies},
  author = {Kristen Mazur and Mutiara Sondjaja and Matthew Wright and Carolyn Yarnall},
  year = {2022},
  eprint = {2008.01749},
  archivePrefix = {arXiv}
}

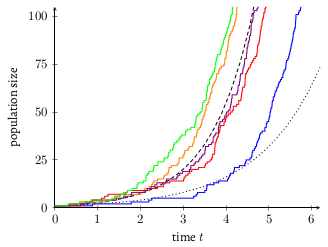
Bacterial Growth: Not So Simple

John Chase and Matthew Wright

to appear in Mathematics Magazine (October 2023)

preprint copy (2021)

Abstract Bibtex

Bacterial growth is used as a simple example of exponential growth, but a population often grows much faster than the average time-to-division suggests. We examine the effect of randomness in the time-to-division of individual bacteria and the aggregate population growth, revealing intricacies that are often overlooked. Specifically, the average time-to-division of individual bacteria does not by itself determine the aggregate population growth. Exponential population growth occurs in realistic scenarios, but the aggregate growth factor depends in non-obvious ways on the underlying splitting distribution.

@misc{Chase_Wright_2021,
  title = {Bacterial Growth: Not So Simple},
  author = {John Chase and Matthew Wright},
  journal = {Mathematics Magazine},
  year = {2023},
  doi = {https://doi.org/10.1080/0025570X.2023.2232259} }

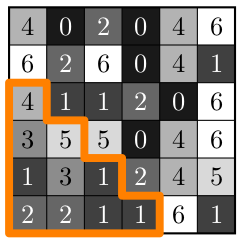
Value-Offset Bifiltrations for Digital Images

Anway De, Thong Vo, and Matthew Wright

published in Computational Geometry (February 2023)

preprint on arxiv.org (2022)

Abstract Bibtex

Persistent homology, an algebraic method for discerning structure in abstract data, relies on the construction of a sequence of nested topological spaces known as a filtration. Two-parameter persistent homology allows the analysis of data simultaneously filtered by two parameters, but requires a bifiltration -- a sequence of topological spaces simultaneously indexed by two parameters. To apply two-parameter persistence to digital images, we first must consider bifiltrations constructed from digital images, which have scarcely been studied. We introduce the value-offset bifiltration for grayscale digital image data. We present efficient algorithms for computing this bifiltration with respect to the taxicab distance and for approximating it with respect to the Euclidean distance. We analyze the runtime complexity of our algorithms, demonstrate the results on sample images, and contrast the bifiltrations obtained from real images with those obtained from random noise.

@misc{De_Vo_Wright_2022,
  title = {Value-Offset Bifiltrations for Digital Images},
  author = {Anway De and Thong Vo and Matthew Wright},
  journal = {Computational Geometry},
  volume = {109},
  pages = {101939},
  year = {2023},
  issn = {0925-7721},
  doi = {https://doi.org/10.1016/j.comgeo.2022.101939} }

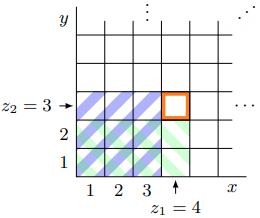
Computing Minimal Presentations and Bigraded Betti Numbers of 2-Parameter Persistent Homology

Michael Lesnick and Matthew Wright

published in SIAM Journal on Applied Algebra and Geometry (2022)

preprint on arxiv.org (2020)

Abstract Bibtex

Motivated by applications to topological data analysis, we give an efficient algorithm for computing a (minimal) presentation of a bigraded \(K[x,y]\)-module \(M\), where \(K\) is a field. The algorithm takes as input a short chain complex of free modules \[ F^2 \xrightarrow{\partial^2} F^1 \xrightarrow{\partial^1} F^0 \] such that \(M \cong \ker{\partial^1}/\mathrm{im}{\partial^2}\). It runs in time \(O(\sum_i |F^i|^3)\) and requires \(O(\sum_i |F^i|^2)\) memory, where \(|F^i|\) denotes the size of a basis of \(F^i\). We observe that, given the presentation computed by our algorithm, the bigraded Betti numbers of \(M\) are readily computed. Our algorithm has been implemented in RIVET, a software tool for the visualization and analysis of two-parameter persistent homology. In experiments on topological data analysis problems, our implementation outperforms the standard computational commutative algebra packages Singular and Macaulay2 by a wide margin.

@misc{Lesnick_Wright_2020,
  title = {Computing Minimal Presentations and Bigraded Betti Numbers of 2-Parameter Persistent Homology},
  author = {Michael Lesnick and Matthew Wright},
  journal = {SIAM Journal on Applied Algebra and Geometry},
  volume = 6,
  number = 2,
  pages = {267-298}
  year = {2022},
  doi = {10.1137/20M1388425}
}

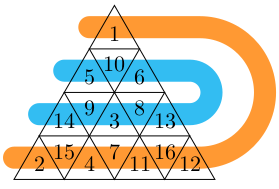
Magic Triangles

Gabriel Hale, Bjorn Vogen, and Matthew Wright

published in The Pi Mu Epsilon Journal (Fall 2021)

preprint copy (2021)

Abstract Bibtex

Magic squares are well-known arrangements of integers with common row, column, and diagonal sums. Various other magic shapes have been proposed, but triangles have been somewhat overlooked. We introduce certain triangular arrangements of integers with common sums in three directions, which we call magic triangles. For small sizes of these triangles, we count the number of unique magic triangles and examine distributions of integers at different positions within them. While we cannot enumerate the number of magic triangles at larger sizes, we offer a simulated annealing method for finding magic triangles.

@article{Hale_Vogen_Wright_2021,
  title = {Magic Triangles},
  author = {Hale, Gabriel and Vogen, Bjorn and Wright, Matthew},
  journal = {The Pi Mu Epsilon Journal},
  volume = 15,
  number = 1,
  year = 2021,
  pages = {265-273}
}

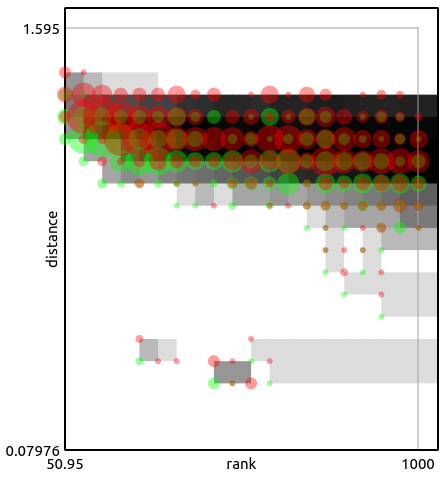
Topological Data Analysis of Simple English Wikipedia Articles

Matthew Wright and Xiaojun Zheng

published in PUMP Journal of Undergraduate Research (2020)

preprint on arxiv.org

Abstract Bibtex

Single-parameter persistent homology, a key tool in topological data analysis, has been widely applied to data problems along with statistical techniques that quantify the significance of the results. In contrast, statistical techniques for two-parameter persistence, while highly desirable for real-world applications, have scarcely been considered. We present three statistical approaches for comparing geometric data using two-parameter persistent homology; these approaches rely on the Hilbert function, matching distance, and barcodes obtained from two-parameter persistence modules computed from the point-cloud data. Our statistical methods are broadly applicable for analysis of geometric data indexed by a real-valued parameter. We apply these approaches to analyze high-dimensional point-cloud data obtained from Simple English Wikipedia articles. In particular, we show how our methods can be utilized to distinguish certain subsets of the Wikipedia data and to compare with random data. These results yield insights into the construction of null distributions and stability of our methods with respect to noisy data.

@article{Wright_Zheng_2020,
  title = {Topological Data Analysis on Simple English Wikipedia Articles},
  author = {Wright, Matthew and Zheng, Xiaojun},
  journal = {The PUMP Journal of Undergraduate Research},
  volume = 3,
  year = 2020,
  month = {Dec.},
  pages = {308-328},
  url = {https://journals.calstate.edu/pump/article/view/2410}
}

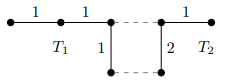
Finding Minimum Spanning Forests in a Graph

Abdel-Rahman Madkour, Phillip Nadolny, Matthew Wright

published in Proceedings of MICS 2019

preprint on arxiv.org

Abstract Bibtex

We introduce a graph partitioning problem motivated by computational topology and propose two algorithms that produce approximate solutions. Specifically, given a weighted, undirected graph G and a positive integer k, we desire to find k disjoint trees within G such that each vertex of G is contained in one of the trees and the weight of the largest tree is as small as possible. We are unable to find this problem in the graph partitioning literature, but we show that the problem is NP-complete. We then propose two approximation algorithms, one that uses a spectral clustering approach and another that employs a dynamic programming strategy, which produce near-optimal partitions on a family of test graphs. We describe these algorithms and analyze their empirical performance.

@article{Madkour_Nadolny_Wright_2019,
  author = {Abdel-Rahman Madkour and Phillip Nadolny and Matthew Wright},
  title = {Finding Minimal Spanning Forests in a Graph},
  booktitle = {The 2019 Midwest Instruction and Computing Symposium},
  year = 2019,
  url = {http://www.micsymposium.org/mics2019/online-proceedings/}
}

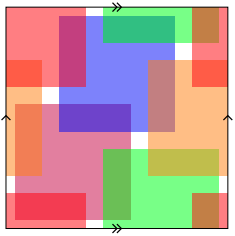
Approval Voting in Product Societies

Kristen Mazur, Mutiara Sondjaja, Matthew Wright, and Carolyn Yarnall

published in The American Mathematical Monthly (2018)

preprint on arxiv.org

Abstract Bibtex

In approval voting, individuals vote for all platforms that they find acceptable. In this situation it is natural to ask: When is agreement possible? What conditions guarantee that some fraction of the voters agree on even a single platform? Berg et. al. found such conditions when voters are asked to make a decision on a single issue that can be represented on a linear spectrum. In particular, they showed that if two out of every three voters agree on a platform, there is a platform that is acceptable to a majority of the voters. Hardin developed an analogous result when the issue can be represented on a circular spectrum. We examine scenarios in which voters must make two decisions simultaneously. For example, if voters must decide on the day of the week to hold a meeting and the length of the meeting, then the space of possible options forms a cylindrical spectrum. Previous results do not apply to these multi-dimensional voting societies because a voter’s preference on one issue often impacts their preference on another. We present a general lower bound on agreement in a two-dimensional voting society, and then examine specific results for societies whose spectra are cylinders and tori.

@article{Mazur_EtAl_2018,
  author = {Kristen Mazur and Mutiara Sondjaja and Matthew Wright and   Carolyn Yarnall},
  title = {Approval Voting in Product Societies},
  journal = {The American Mathematical Monthly},
  volume = 125,
  number = 1,
  pages = {29-43},
  year = 2018,
  doi = {10.1080/00029890.2018.1390370},
}

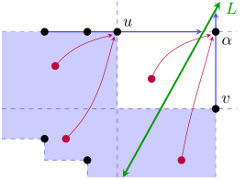
Interactive Visualization of 2-D Persistence Modules

Michael Lesnick and Matthew Wright

preprint on arxiv.org (2015)

Abstract Bibtex

The goal of this work is to extend the standard persistent homology pipeline for exploratory data analysis to the 2-D persistence setting, in a practical, computationally efficient way. To this end, we introduce RIVET, a software tool for the visualization of 2-D persistence modules, and present mathematical foundations for this tool. RIVET provides an interactive visualization of the barcodes of 1-D affine slices of a 2-D persistence module M. It also computes and visualizes the dimension of each vector space in M and the bigraded Betti numbers of M. At the heart of our computational approach is a novel data structure based on planar line arrangements, on which we can perform fast queries to find the barcode of any slice of M. We present an efficient algorithm for constructing this data structure and establish bounds on its complexity.

@misc{Lesnick_Wright_2015,
  title = {Interactive Visualization of 2-D Persistence Modules},
  author = {Michael Lesnick and Matthew Wright},
  year = 2015,
  eprint = {1512.00180},
  archivePrefix = {arXiv}
}

Towards Domain-Specific Semantic Relatedness: A Case Study from Geography

Shilad Sen, Isaac Johnson, Rebecca Harper, Huy Mai, Samuel Horlbeck Olsen, Benjamin Mathers, Laura Souza Vonessen, Matthew Wright, and Brent Hecht

published copy in Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence (IJCAI 2015)

Abstract Bibtex

Semantic relatedness (SR) measures form the algorithmic foundation of intelligent technologies in domains ranging from artificial intelligence to human-computer interaction. Although SR has been researched for decades, this work has focused on developing general SR measures rooted in graph and text mining algorithms that perform reasonably well for many different types of concepts. This paper introduces domain-specific SR, which augments general SR by identifying, capturing, and synthesizing domain-specific relationships between concepts. Using the domain of geography as a case study, we show that domain-specific SR — and even geography-specific signals alone (e.g. distance, containment) without sophisticated graph or text mining algorithms — significantly outperform the SR state-of-the-art for geographic concepts. In addition to substantially improving SR measures for geospatial technologies, an area that is rapidly increasing in importance, this work also unlocks an important new direction for SR research: SR measures that incorporate domain-specific customizations to increase accuracy.

@inproceedings{ url = https://www.ijcai.org/Abstract/15/334 }

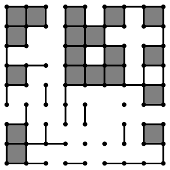
Intrinsic Volumes of Random Cubical Complexes

Michael Werman and Matthew Wright

published copy in Discrete and Computational Geometry (2016)

preprint copy on arxiv.org

Abstract Bibtex

Intrinsic volumes, which generalize both Euler characteristic and Lebesgue volume, are important properties of d-dimensional sets. A random cubical complex is a union of unit cubes, each with vertices on a regular cubic lattice, constructed according to some probability model. We analyze and give exact polynomial formulae, dependent on a probability, for the expected value and variance of the intrinsic volumes of several models of random cubical complexes. We then prove a central limit theorem for these intrinsic volumes. For our primary model, we also prove an interleaving theorem for the zeros of the expected-value polynomials. The intrinsic volumes of cubical complexes are useful for understanding the shape of random d-dimensional sets and for characterizing noise in applications.

@article{Werman_Wright_2016,   author = {Michael Werman and Matthew Wright},
  title = {Intrinsic Volumes of Random Cubical Complexes},
  journal = {Discrete and Computational Geometry},
  year = 2016,
  number = 2,
  pages = {201-213},
  month = 7,
  volume = 4
}

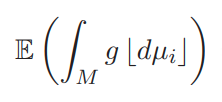
Hadwiger Integration of Random Fields

Matthew Wright

published copy in Topological Methods in Nonlinear Analysis (2015)

preprint copy on arxiv.org

Abstract Bibtex

Hadwiger integrals employ the intrinsic volumes as measures for integration of real-valued functions. We provide a formula for the expected values of Hadwiger integrals of Gaussian-related random fields. The expected Hadwiger integrals of random fields are both theoretically interesting and potentially useful in applications such as sensor networks, image processing, and cell dynamics. Furthermore, combining the expected integrals with a functional version of Hadwiger's theorem, we obtain expected values of more general valuations on Gaussian-related random fields.

@article{Wright_2015,   author = {Matthew Wright},
  title = {Hadwiger Integration of Random Fields},
  journal = {Topological Methods in Nonlinear Analysis},
  year = 2015,
  number = 1,
  pages = {117-128},
  month = 3,
  volume = 45
}

A Hadwiger Theorem for Simplicial Maps

P. Christopher Staecker and Matthew Wright

preprint copy on arxiv.org (2014)

Abstract Bibtex

We define the notion of valuation on simplicial maps between geometric realizations of simplicial complexes in \(\mathbb{R}^n\). Valuations on simplicial maps are analogous to valuations on sets. In particular, we define the Lefschetz volumes, which are analogous to the intrinsic volumes of subsets of \(\mathbb{R}^n\). Our definition not only provides a generalization of the Lefschetz number, but also yields a Hadwiger-style classification theorem for all such valuations.

@misc{Staecker_Wright_2015,
  title = {A Hadwiger Theorem for Simplicial Maps},
  author = {P. Christopher Staecker and Matthew Wright},
  year = 2014,
  eprint = {1402.6391},
  archivePrefix = {arXiv}
}

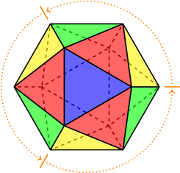
Colorful Symmetries

Brian Bargh, John Chase, and Matthew Wright

published copy in Math Horizons (2014)

preprint copy

Abstract Bibtex

Burnside’s lemma is the key to solving one of Google’s colorful puzzles. With a focus on the concept of symmetry, this article explains how to count the number of ways that you can color an icosahedron (or another geometric object) with n colors.

@article{Bargh_Chase_Wright_2014,
  title = {Colorful Symmetries},
  author = {Brian Bargh and John Chase and Matthew Wright},
  journal = {Math Horizons},
  number = 4,
  pages = {14--17},
  publisher = {Mathematical Association of America},
  volume = 21,
  year = 2014,
  URL = {http://www.jstor.org/stable/10.4169/mathhorizons.21.4.14}
}

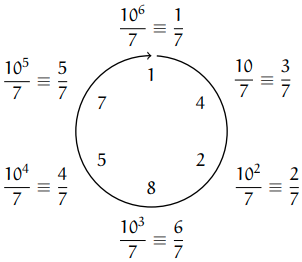
Cycles of Digits

Matthew Wright

preprint copy (2013)

Abstract Bibtex

Cyclic permutations of digits that appear in repeating fractions can help students understand important concepts in abstract algebra.

@unpublished{Wright_2013,
  title = {Cycles of Digits},
  author = {Matthew Wright},
  year = 2014,
  URL = {https://mlwright.org/docs/cycles.pdf}
}

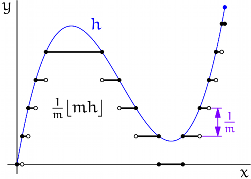
Hadwiger's Theorem for Definable Functions

Yuliy Baryshnikov, Robert Ghrist, and Matthew Wright

published copy in Advances in Mathematics (2013)

preprint copy on arxiv.org

Abstract Bibtex

Hadwiger’s Theorem states that \(\mathbb{E}^n\)-invariant convex-continuous valuations of definable sets in \(\mathbb{R}^n\) are linear combinations of intrinsic volumes. We lift this result from sets to data distributions over sets, specifically, to definable \(\mathbb{R}\)-valued functions on \(\mathbb{R}^n\). This generalizes intrinsic volumes to (dual pairs of) non-linear valuations on functions and provides a dual pair of Hadwiger classification theorems.

@article{Baryshnikov_Ghrist_Wright_2013,   author = {Yuliy Baryshnikov and Robert Ghrist and Matthew Wright},
  title = {Hadwiger's Theorem for Definable Functions},
  journal = {Advances in Mathematics},
  year = 2013,
  pages = {573-586},
  month = 10,
  volume = 245,
  doi = {https://doi.org/10.1016/j.aim.2013.07.001}, }

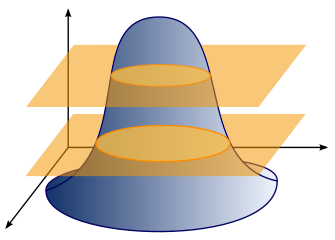
Hadwiger Integration of Definable Functions

Matthew Wright

Publicly Accessible Penn Dissertations, paper 391 (2011)

Abstract Bibtex

This thesis defines and classifies valuations on definable functionals. The intrinsic volumes are valuations on "tame" subsets of \(\mathbb{R}^n\), and by easy extension, valuations on functionals on \(\mathbb{R}^n\) with infinitely many level sets, each a "tame" subset of \(\mathbb{R}^n\). We extend these valuations, which we call Hadwiger integrals, to definable functionals on \(\mathbb{R}^n\), and present some important properties of the valuations. With the appropriate topologies on the set of definable functionals, we obtain dual classification theorems for general valuations on such functionals. We also explore integral transforms, convergence results, and applications of the Hadwiger integrals.

@phdthesis{WrightThesis,
author = "Matthew Wright",
title = "Hadwiger Integration of Definable Functions",
school = "University of Pennsylvania",
address = "Philadelphia, PA",
year = 2011,
number = 391,
url = "https://repository.upenn.edu/edissertations/391"
}